By Dr. Harry Buhrman, Chief Scientist for Algorithms and Innovation, and Dr. Chris Langer, Fellow

This week, we confirm what has been implied by the rapid pace of our recent technical progress as we reveal a major acceleration in our hardware road map. By the end of the decade, our accelerated hardware roadmap will deliver a fully fault-tolerant and universal quantum computer capable of executing millions of operations on hundreds of logical qubits. 

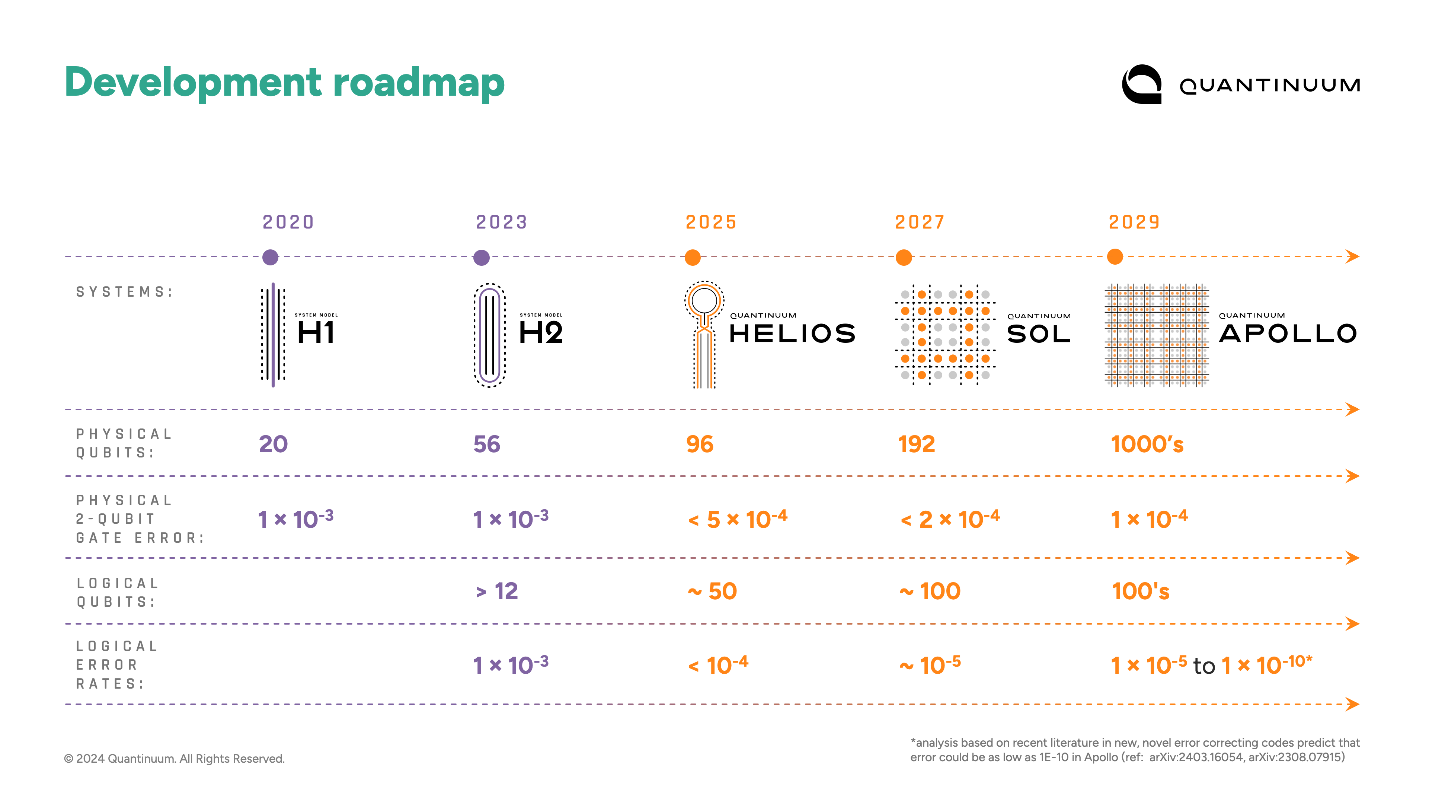
The next major milestone on our accelerated roadmap is Quantinuum Helios™, Powered by Honeywell, a device that will definitively push beyond classical capabilities in 2025. That sets us on a path to our fifth-generation system, Quantinuum Apollo™, a machine that delivers scientific advantage and a commercial tipping point this decade.

What is Apollo?

We are committed to continually advancing the capabilities of our hardware over prior generations, and Apollo makes good on that promise. It will offer:

• thousands of physical qubits
• physical error rates less than 10^-4
• All of our most competitive features: all-to-all connectivity, low crosstalk, mid-circuit measurement and qubit re-use
• Conditional logic
• Real-time classical co-compute
• Physical variable angle 1 qubit and 2 qubit gates
• Hundreds of logical qubits
• Logical error rates better than 10^-6 with analysis based on recent literature estimating as low as 10^-10

By leveraging our all-to-all connectivity and low error rates, we expect to enjoy significant efficiency gains in terms of fault-tolerance, including single-shot error correction (which saves time) and high-rate and high-distance Quantum Error Correction (QEC) codes (which mean more logical qubits, with stronger error correction capabilities, can be made from a smaller number of physical qubits). 

Studies of several efficient QEC codes already suggest we can enjoy logical error rates much lower than our target 10^-6 – we may even be able to reach 10^-10, which enables exploration of even more complex problems of both industrial and scientific interest.

Error correcting code exploration is only just beginning – we anticipate discoveries of even more efficient codes. As new codes are developed, Apollo will be able to accommodate them, thanks to our flexible high-fidelity architecture. The bottom line is that Apollo promises fault-tolerant quantum advantage sooner, with fewer resources.

Like all our computers, Apollo is based on the quantum charged coupled device (QCCD) architecture. Here, each qubit’s information is stored in the atomic states of a single ion. Laser beams are applied to the qubits to perform operations such as gates, initialization, and measurement. The lasers are applied to individual qubits or co-located qubit pairs in dedicated operation zones. Qubits are held in place using electromagnetic fields generated by our ion trap chip. We move the qubits around in space by dynamically changing the voltages applied to the chip. Through an alternating sequence of qubit rearrangements via movement followed by quantum operations, arbitrary circuits with arbitrary connectivity can be executed.

The ion trap chip in Apollo will host a 2D array of trapping locations. It will be fabricated using standard CMOS processing technology and controlled using standard CMOS electronics. The 2D grid architecture enables fast and scalable qubit rearrangement and quantum operations – a critical competitive advantage. The Apollo architecture is scalable to the significantly larger systems we plan to deliver in the next decade.

What is Apollo good for?

Apollo’s scaling of very stable physical qubits and native high-fidelity gates, together with our advanced error correcting and fault tolerant techniques will establish a quantum computer that can perform tasks that do not run (efficiently) on any classical computer. We already had a first glimpse of this in our recent work sampling the output of random quantum circuits on H2, where we performed 100x better than competitors who performed the same task while using 30,000x less power than a classical supercomputer. But with Apollo we will travel into uncharted territory.

The flexibility to use either thousands of qubits for shorter computations (up to 10k gates) or hundreds of qubits for longer computations (from 1 million to 1 billion gates) make Apollo a versatile machine with unprecedented quantum computational power. We expect the first application areas will be in scientific discovery; particularly the simulation of quantum systems. While this may sound academic, this is how all new material discovery begins and its value should not be understated. This era will lead to discoveries in materials science, high-temperature superconductivity, complex magnetic systems, phase transitions, and high energy physics, among other things.

In general, Apollo will advance the field of physics to new heights while we start to see the first glimmers of distinct progress in chemistry and biology. For some of these applications, users will employ Apollo in a mode where it offers thousands of qubits for relatively short computations; e.g. exploring the magnetism of materials. At other times, users may want to employ significantly longer computations for applications like chemistry or topological data analysis. 

But there is more on the horizon. Carefully crafted AI models that interact seamlessly with Apollo will be able to squeeze all the “quantum juice” out and generate data that was hitherto unavailable to mankind. We anticipate using this data to further the field of AI itself, as it can be used as training data. 

The era of scientific (quantum) discovery and exploration will inevitably lead to commercial value. Apollo will be the centerpiece of this commercial tipping point where use-cases will build on the value of scientific discovery and support highly innovative commercially viable products. 

Very interestingly, we will uncover applications that we are currently unaware of. As is always the case with disruptive new technology, Apollo will run currently unknown use-cases and applications that will make perfect sense once we see them. We are eager to co-develop these with our customers in our unique co-creation program.

How do we get there?

Today, System Model H2 is our most advanced commercial quantum computer, providing 56 physical qubits with physical two-qubit gate errors less than 10^-3. System Model H2, like all our systems, is based on the QCCD architecture.

Starting from where we are today, our roadmap progresses through two additional machines prior to Apollo. The Quantinuum Helios™ system, which we are releasing in 2025, will offer around 100 physical qubits with two-qubit gate errors less than 5x10^-4. In addition to expanded qubit count and better errors, Helios makes two departures from H2. First, Helios will use 137Ba+ qubits in contrast to the 171Yb+ qubits used in our H1 and H2 systems. This change enables lower two-qubit gate errors and less complex laser systems with lower cost. Second, for the first time in a commercial system, Helios will use junction-based qubit routing. The result will be a “twice-as-good" system: Helios will offer roughly 2x more qubits with 2x lower two-qubit gate errors while operating more than 2x faster than our 56-qubit H2 system.

After Helios we will introduce Quantinuum Sol™, our first commercially available 2D-grid-based quantum computer. Sol will offer hundreds of physical qubits with two-qubit gate errors less than 2x10^-4, operating approximately 2x faster than Helios. Sol being a fully 2D-grid architecture is the scalability launching point for the significant size increase planned for Apollo.

Opportunity for early value creation discovery in Helios and Sol

Thanks to Sol’s low error rates, users will be able to execute circuits with up to 10,000 quantum operations. The usefulness of Helios and Sol may be extended with a combination of quantum error detection (QED) and quantum error mitigation (QEM). For example, the [[k+2, k, 2]] iceberg code is a light-weight QED code that encodes k+2 physical qubits into k logical qubits and only uses an additional 2 ancilla qubits. This low-overhead code is well-suited for Helios and Sol because it offers the non-Clifford variable angle entangling ZZ-gate directly without the overhead of magic state distillation. The errors Iceberg fails to detect are already ~10x lower than our physical errors, and by applying a modest run-time overhead to discard detected failures, the effective error in the computation can be further reduced. Combining QED with QEM, a ~10x reduction in the effective error may be possible while maintaining run-time overhead at modest levels and below that of full-blown QEC.

Why accelerate our roadmap now?

Our new roadmap is an acceleration over what we were previously planning. The benefits of this are obvious: Apollo brings the commercial tipping point sooner than we previously thought possible. This acceleration is made possible by a set of recent breakthroughs.

First, we solved the “wiring problem”: we demonstrated that trap chip control is scalable using our novel center-to-left-right (C2LR) protocol and broadcasting shared control signals to multiple electrodes. This demonstration of qubit rearrangement in a 2D geometry marks the most advanced ion trap built, containing approximately 40 junctions. This trap was deployed to 3 different testbeds in 2 different cities and operated with 2 different collections of dual-ion-species, and all 3 cases were a success. These demonstrations showed that the footprint of the most complex parts of the trap control stay constant as the number of qubits scales up. This gives us the confidence that Sol, with approximately 100 junctions, will be a success.

Second, we continue to reduce our two-qubit physical gate errors. Today, H1 and H2 have two-qubit gate errors less than 1x10^-3 across all pairs of qubits. This is the best in the industry and is a key ingredient in our record >2 million quantum volume. Our systems are the most benchmarked in the industry, and we stand by our data - making it all publicly available. Recently, we observed an 8x10^-4 two-qubit gate error in our Helios development test stand in 137Ba+, and we’ve seen even better error rates in other testbeds. We are well on the path to meeting the 5x10^-4 spec in Helios next year.

Third, the all-to-all connectivity offered by our systems enables highly efficient QEC codes. In Microsoft’s recent demonstration, our H2 system with 56 physical qubits was used to generate 12 logical qubits at distance 4. This work demonstrated several experiments, including repeated rounds of error correction where the error in the final result was ~10x lower than the physical circuit baseline.

In conclusion, through a combination of advances in hardware readiness and QEC, we have line-of-sight to Apollo by the end of the decade, a fully fault-tolerant quantum advantaged machine. This will be a commercial tipping point: ushering in an era of scientific discovery in physics, materials, chemistry, and more. Along the way, users will have the opportunity to discover new enabling use cases through quantum error detection and mitigation in Helios and Sol.

Quantinuum has the best quantum computers today and is on the path to offering fault-tolerant useful quantum computation by the end of the decade.

Quantinuum is uniquely known for, and has always put a premium on, demonstrating rather than merely promising breakthroughs in quantum computing. 

When we unveiled the first H-Series quantum computer in 2020, not only did we pioneer the world-leading quantum processors, but we also went the extra mile. We included industry leading comprehensive benchmarking to ensure that any expert could independently verify our results. Since then, our computers have maintained the lead against all competitors in performance and transparency. Today our System Model H2 quantum computer with 56 qubits is the most powerful quantum computer available for industry and scientific research – and the most benchmarked. 

More recently, in a period where we upgraded our H2 system from 32 to 56 qubits and demonstrated the scalability of our QCCD architecture, we also hit a quantum volume of over two million, and announced that we had achieved “three 9’s” fidelity, enabling real gains in fault-tolerance – which we proved within months as we demonstrated the most reliable logical qubits in the world with our partner Microsoft. 

We don’t just promise what the future might look like; we demonstrate it.

Today, at Quantum World Congress, we shared how recent developments by our integrated hardware and software teams have, yet again, accelerated our technology roadmap. It is with the confidence of what we’ve already demonstrated that we can uniquely announce that by the end of this decade Quantinuum will achieve universal fully fault-tolerant quantum computing, built on foundations such as a universal fault-tolerant gate set, high fidelity physical qubits uniquely capable of supporting reliable logical qubits, and a fully-scalable architecture.

We also demonstrated, with Microsoft, what rapid acceleration looks like with the creation of 12 highly reliable logical qubits – tripling the number from just a few months ago. Among other demonstrations, we supported Microsoft to create the first ever chemistry simulation using reliable logical qubits combined with Artificial Intelligence (AI) and High-Performance Computing (HPC), producing results within chemical accuracy. This is a critical demonstration of what Microsoft has called “the path to a Quantum Supercomputer”. 

Quantinuum’s H-Series quantum computers, Powered by Honeywell, were among the first devices made available via Microsoft Azure, where they remain available today. Building on this, we are excited to share that Quantinuum and Microsoft have completed integration of Quantinuum’s InQuanto™ computational quantum chemistry software package with Azure Quantum Elements, the AI enabled generative chemistry platform. The integration mentioned above is accessible to customers participating in a private preview of Azure Quantum Elements, which can be requested from Microsoft and Quantinuum.  

We created a short video on the importance of logical qubits, which you can see here:

These demonstrations show that we have the tools to drive progress towards scientific and industrial advantage in the coming years. Together, we’re demonstrating how quantum computing may be applied to some of humanity’s most pressing problems, many of which are likely only to be solved with the combination of key technologies like AI, HPC, and quantum computing. 

Our credible roadmap draws a direct line from today to hundreds of logical qubits - at which point quantum computing, possibly combined with AI and HPC, will outperform classical computing for a range of scientific problems. 

“The collaboration between Quantinuum and Microsoft has established a crucial step forward for the industry and demonstrated a critical milestone on the path to hybrid classical-quantum supercomputing capable of transforming scientific discovery.” – Dr. Krysta Svore – Technical Fellow and VP of Advanced Quantum Development for Microsoft Azure Quantum

What we revealed today underlines the accelerating pace of development. It is now clear that enterprises need to be ready to take advantage of the progress we can see coming in the next business cycle.

Why now?

The industry consensus is that the latter half of this decade will be critical for quantum computing, prompting many companies to develop roadmaps signalling their path toward error corrected qubits. In their entirety, Quantinuum’s technical and scientific advances accelerate the quantum computing industry, and as we have shown today, reveal a path to universal fault-tolerance much earlier than expected.

Grounded in our prior demonstrations, we now have sufficient visibility into an accelerated timeline for a highly credible hardware roadmap, making now the time to release an update. This provides organizations all over the world with a way to plan, reliably, for universal fully fault-tolerant quantum computing. We have shown how we will scale to more physical qubits at fidelities that support lower error rates (made possible by QEC), with the capacity for “universality” at the logical level. “Universality” is non-negotiable when making good on the promise of quantum computing: if your quantum computer isn’t universal everything you do can be efficiently reproduced on a classical computer. 

“Our proven history of driving technical acceleration, as well as the confidence that globally renowned partners such as Microsoft have in us, means that this is the industry’s most bankable roadmap to universal fully fault-tolerant quantum computing,” said Dr. Raj Hazra, Quantinuum’s CEO.

Where we go from here?

Before the end of the decade, our quantum computers will have thousands of physical qubits, hundreds of logical qubits with error rates less than 10^-6, and the full machinery required for universality and fault-tolerance – truly making good on the promise of quantum computing. 

Quantinuum has a proven history of achieving our technical goals. This is evidenced by our leadership in hardware, software, and the ecosystem of developer tools that make quantum computing accessible. Our leadership in quantum volume and fidelity, our consistent cadence of breakthrough publications, and our collaboration with enterprises such as Microsoft, showcases our commitment to pushing the boundaries of what is possible. 

We are now making an even stronger public commitment to deliver on our roadmap, ushering the industry toward the era of universal fully fault-tolerant quantum computing this decade. We have all the machinery in place for fault-tolerance with error rates around 10^-6, meaning we will be able to run circuits that are millions of gates deep – putting us on a trajectory for scientific quantum advantage, and beyond. 

Every year, The IEEE International Conference on Quantum Computing and Engineering – or IEEE Quantum Week – brings together engineers, scientists, researchers, students, and others to learn about advancements in quantum computing.

At this year’s conference from September 15^th – 20^th, the Quantinuum team shared insights on how we are forging the path to fault-tolerant quantum computing with our integrated full-stack. Check out our CEO, Dr. Rajeeb Hazra's keynote address to discover how Quantinuum will deliver universal, fully fault-tolerant quantum computing by the end of the decade: 

‍

The below sessions will be available to view on-demand soon. Stay tuned to learn about recent upgrades to our hardware, our path to error correction, enhancements to our open-source toolkits, and more.

Sunday, September 15

Workshop: Towards Error Correction within Modular Quantum Computing Architectures‍

Speaker: Henry Semenenko, Senior Advanced Optics Engineer

Time: 10:00 – 16:30

QSEEC: High schoolers excel at Oxford post-graduate quantum exam: experimental evidence in support of quantum picturalism

Speakers: Bob Coecke, Chief Scientist, chaired by Lia Yeh, Research Engineer, who is chair of Quantum in K-12 and Quantum Understanding sessions

Time: 13:00 – 13:15

Monday, September 16

Birds of a Feather: AI in Quantum Computing

Speaker: Josh Savory, Director of Offering Management, Hardware and Cloud Platform Products

Time: 10:00 – 11:30

Tutorial: Using and benefiting from Quantinuum H-Series quantum computers’ unique features

Speakers: Irfan Khan, Senior Application Engineer, and Shival Dasu, Advanced Physicist

Time: 13:00 – 16:30

Tuesday, September 17

Workshop: Applications Explored on H-Series Quantum Hardware

Speakers: Michael Foss-Feig, Principal Physicist, and Nathan Fitzpatrick, Senior Research Scientist

Time: 10:00 – 16:30

Panel: How Microsoft and Quantinuum built on decades of research to achieve the most reliable logical qubits on record

Speakers: Josh Savory, Director of Offering Management, Hardware and Cloud Platform Products, and David Hayes, Senior R&D Manager for the theory and architecture groups

Time: 10:00 – 11:30

Panel: The Role of Error Suppression, Mitigation and Correction in Reaching the First Algorithmic Quantum Advantages

Speaker: Michael Foss-Feig, Principal Physicist

Time: 15:00 – 16:30

Thursday, September 19

Keynote: Quantinuum H-Series: Advancing Quantum Computing to Scalable Fault-Tolerant Systems

Speaker: Rajeeb Hazra, President & Chief Executive Officer

Time: 8:00 – 9:00

Workshop: Current Progress and Remaining Challenges in Scaling Trapped-Ion Quantum Computing

Speaker: Robert Delaney, Advanced Physicist

Time: 10:00 – 16:30

Tutorial: From Quantum in Pictures to Interpretable Quantum NLP

Speakers: Bob Coecke, Chief Scientist, and Lia Yeh, Research Engineer

Time: 13:00 – 16:30

Workshop: Quantum Software 2.0: Enabling Large-scale and Performant Quantum Computing

Speaker: Kartik Singhal, Quantum Compiler Engineer

Time: 10:00 – 16:30

Birds of a Feather: Navigating the Quantum Computing Journey: Student to Professional Opportunities

Speaker: Lia Yeh

Time: 10:00 – 11:30

Friday, September 20

Workshop: Academic and professional training in quantum computing: the importance of open-source

Speaker: Lia Yeh, Research Engineer

Time: 10:00 – 16:30

Panel: What Does “Break Even” Mean?

Speaker: David Hayes, Senior R&D Manager for the theory and architecture groups

Time: 10:00 – 11:30

*All sessions are listed in Montreal time, Eastern Daylight Time

Quantinuum is excited to introduce the beta availability of Quantinuum Nexus, our comprehensive quantum computing platform. Nexus is built to simplify quantum computing workflows with its expert design and full-stack support. We are inviting quantum users to apply for beta availability; accepted users can work closely with Quantinuum on how Nexus can be adopted and customized for you.

Nexus was developed by our in-house quantum experts to streamline the deployment of quantum algorithms. From tackling common tasks like installing packages and libraries to addressing pain points like setting up storage, Nexus seamlessly integrates thoughtful details to enhance user experience. 

Run, track, and manage your usage

Nexus allows users to run, track, and manage resources across multiple quantum backends, making it easier for researchers to directly compare results and processes when using our H-Series hardware or other providers. Additionally, Nexus features a cloud-hosted and preconfigured JupyterHub environment and dedicated simulators - most notably, the Quantinuum H-Series emulator. Nexus’ emulator integration means that new users and organizations that don’t have access to H-Series hardware can start experimenting with H-Series capabilities right away.

Full-stack mindset

Quantinuum Nexus is at the core of our full stack, integrated fully with our H-Series Quantum Processor, our software offerings such as InQuanto™, and our H-Series emulators. Nexus is also back-end inclusive, interfacing with multiple other hardware and simulation backends. In the future, we will be introducing new cutting-edge tools such as a more powerful cloud-based version of our compiler, powered by version 2 of TKET.

Nexus also stores everything you need to recreate your experiment in one place – meaning a full snapshot of the backend, the settings and variables you used, and more. Combined with easy data sharing and storage, you can stop worrying about the logistics of data management. You’re in control of how you structure your data, how you track what’s most important to you, and who gets to see it.

Tools for Administrators

Administrators benefit from resource controls within Nexus, allowing them to manage user access, create user groups, and update usage quotas to match their priorities. With multiple backend support, administrators can track jobs and usage for all their quantum resource in one platform. Advanced usage visualization allows administrators to quickly gain insight from historical trends in usage. Nexus also features collaboration tools that give users the ability to share data, as well as access controls that allow administrators to ensure this is done securely.

Why Quantinuum Nexus?

Users, developers, and administrators have several options when it comes to selecting a platform for managing quantum resources. So why Nexus? Quantinuum Nexus was built by quantum experts, for quantum experts. Our experiment management and cataloging system makes us stand out as the best platform for collaborating between scientific teams. Our provision of the H-Series emulator in the cloud means you get more access to the emulator of one of the world's best devices with less time in the queue, so you can spend more time with your results. Our quantum chemistry package InQuanto™ is integrated into Nexus, meaning zero setup time with easy data storage in our managed environment.

Nexus provides a consistent API for working with a range of quantum devices & tools. This improves the experience of our end users, as scripts that work for one device can easily be ported to other devices with only a change to the config. The Nexus API interface also improves integration with 3^rd party partners by providing them a programmatic way to access Quantinuum tools, alongside a pathway for integrating these resources into their own tools for redistribution.

With Nexus, Quantinuum is setting a new standard in quantum Platform-as-a-Service providers, empowering users with cutting-edge tools and seamless integration for quantum computing advancements.

Communication is the connective tissue of society, weaving individuals into groups and communities and mediating the progress and development of culture. The technology of communications evolves continuously, occasionally undergoing paradigm shifts such as those brought about by the Gutenberg press and broadcast television.

From historical examples such as the proliferation of fast merchant trading ships, to the modern telecommunications networks spread across the world via a web of cables buried under the sea floor and satellites thousands of kilometres high, the need for better communication infrastructure has driven some of our most ambitious technologies to date. 

Today, emerging quantum technologies are poised to revolutionise the field of communication once again. They promise new and incredibly valuable opportunities for dependable and secure communications between people, communities, companies, and governments everywhere. Our ability to understand and control quantum systems has opened a new world of exciting possibilities. Soon we might build long-distance quantum communication links and networks, eventually leading to what is known as the quantum internet. 

While some embryonic quantum communication systems are already in place, realisation of their full potential will require significant technological advances. With engineering teams around the world working at pace to deliver this promise across industrial sectors, the need to invest in expert knowledge is rising. 

NASA has been a pioneer in space-based communication over many decades, and more recently has emerged as a leader in space-based quantum communication, dedicating new resources for scientists, engineers and communication systems experts to learn about the field.

Recently, NASA’s Space Communications and Navigation (SCaN) program commissioned a booklet titled Quantum Communication 101, authored by several of our team at Quantinuum. This will be a go-to resource for the global community of scientists and experts that NASA supports, but importantly it has been written so that it requires almost no prior technical knowledge while providing a rigorous account of the emerging field of quantum communications.

What follows is a taster of what’s in Quantum Communication 101.

What is quantum communication?

For the words I am typing now to reach your computer screen, I need to rely on modern communication networks. My laptop memory, Wi-Fi router and communication channels rely on the physics of things like transistors, currents, and radio waves which obey the more familiar, “classical" laws of physics. 

The field of quantum communication, however, relies on the counterintuitive rules of quantum physics. Thanks to incredible feats of engineering, in place of continuous beams of light from diodes, we can now control individual photons to send and receive quantum information. By taking advantage of the peculiar quantum phenomena that they exhibit, like superposition and entanglement, new possibilities are emerging which were previously unimaginable. 

Cutting-edge applications 

In the growing landscape of potential applications in quantum communication, cybersecurity is already deeply rooted. At Quantinuum, for example, quantum computers are used to generate randomness, the fundamental building block of secure encryption. Elsewhere, prototype quantum networks for secure communications already span metropolitan areas. 

As our techniques in quantum communication advance, we may unlock new possibilities in quantum computing, which promises to solve problems too difficult even for supercomputers, and quantum metrology, which will enable measurements at an unprecedented precision. Quantum states of light have already been used in LIGO - a large-scale experiment operated by CalTech and MIT to detect ripples in the fabric of space-time itself.

Connecting the dots: towards a quantum internet 

The end goal of quantum communication is what many refer to as the quantum internet, through which we will seamlessly send quantum signals across many quantum networks. This will be an enormous engineering challenge, requiring international collaboration and the evolution of our existing infrastructure.

Although the exact form that this network will take is yet unknown, we can say with confidence that it will need to pass through space. Much like satellites help to globally connect the Internet, the launch of quantum-capable satellites will play a vital role in a global quantum internet. 

Building a quantum ecosystem

The path to a quantum internet will depend on growing a diverse and expert workforce. This is well understood by bodies such as the National Science Foundation who recently announced a $5.1M Center for Quantum Networks aimed at architecting the quantum internet. Over the last few years, we have seen growing investment worldwide, such as the $1.1B Quantum Technology Flagship in Europe and the $11B Chinese National Laboratory for Quantum Information Science. Important industrial investments are being made by large corporations such as IBM, Google, Intel, Honeywell, Cisco, Amazon, and Microsoft.

Amongst this surge in interest, NASA’s SCaN program has proposed a series of mission concepts for building and testing infrastructure for space-based quantum communication. These include launching satellites capable of sending and receiving quantum signals between ground stations and eventually other satellites. These quantum signals may be entangled photons – a feature that will play an extremely important role in future networks. One such mission concept is shown below, where a quantum-capable satellite with a source of entangled photons connects an intercontinental quantum network.

The second quantum revolution is at an exciting precipice where our ability to transmit quantum information, both on Earth and in space, will be pivotal. Whilst our evolving quantum technologies already show a great deal of promise, it is perhaps the ground-breaking applications that we are yet to discover which will ultimately determine our success. 

It is more important than ever that we support education and collaboration in advancing quantum technologies. Quantum Communication 101 aims to be a starting point for a general audience looking to learn about the topic for the first time, as well as those who wish to explore in detail the technologies that will make the first quantum networks a reality.

‍If you would like to better understand the exciting prospects of quantum communication, you can find the Quantum Communication 101 booklet on the NASA SCaN website. 

Quantum computing promises to help us understand chemistry in its purest form – ultimately leading to a better understanding of everything from drug development to superconductors. But before we can do any of that, researchers in computational quantum chemistry have to create the basic building blocks for understanding a chemical system: they must prepare the initial state of a system, apply various effects to the system through time, then measure the resulting output. 

The first problem, called “state preparation” is a tricky one – researchers have been leaning heavily on “variational” techniques to do this, but those techniques come with huge optimization costs in addition to serious scaling issues for larger systems. An older technique, called “adiabatic state preparation” promises significant speedups on quantum computers vs classical computers, but has been mostly abandoned by researchers because the typical method used for time evolution is costly and introduces too much noise. This method, called “Trotterized adiabatic time evolution”, involves splitting up time into discrete steps, which requires many, many gates, and ultimately needs error rates well out of reach for any near-term quantum computer.

Recently, researchers at Quantinuum found a way around that roadblock – they eliminated the noisy time evolution in favor of a clever averaging approach. Rather than taking a bunch of discrete time steps they simulate different interactions such that on average you get exactly the right time evolution. A nice aspect of this approach is that it has guaranteed “convergence” – ultimately this means that, unlike other approaches, it works all the time. This new approach has also been shown to be possible on near-term quantum computers: it does not require too many gates or computational time, and it scales well with the system size. 

This algorithm is designed with Quantinuum’s world-leading hardware in mind, as it requires all-to-all connectivity. Combined with our industry-leading gate fidelities, this new approach is opening the door to many fascinating applications in chemistry, physics, and beyond.