

Untangling the Mysteries of Knots with Quantum Computers
What Quantum Advantage actually looks like
One of the greatest privileges of working directly with the world’s most powerful quantum computer at Quantinuum is building meaningful experiments that convert theory into practice. The privilege becomes even more compelling when considering that our current quantum processor – our H2 system – will soon be enhanced by Helios, a quantum computer potentially a stunning trillion times more powerful, and due for launch in just a few months. The moment has now arrived when we can build a timeline for applications that quantum computing professionals have anticipated for decades and which are experimentally supported.
Quantinuum’s applied algorithms team has released an end-to-end implementation of a quantum algorithm to solve a central problem in knot theory. Along with an efficiently verifiable benchmark for quantum processors, it allows for concrete resource estimates for quantum advantage in the near-term. The research team, included Quantinuum researchers Enrico Rinaldi, Chris Self, Eli Chertkov, Matthew DeCross, David Hayes, Brian Neyenhuis, Marcello Benedetti, and Tuomas Laakkonen of the Massachusetts Institute of Technology. In this article, Konstantinos Meichanetzidis, a team leader from Quantinuum’s AI group who led the project, writes about the problem being addressed and how the team, adopting an aggressively practical mindset, quantified the resources required for quantum advantage:
Knot theory is a field of mathematics called ‘low-dimensional topology’, with a rich history, stemming from a wild idea proposed by Lord Kelvin, who conjectured that chemical elements are different knots formed by vortices in the aether. Of course, we know today that the aether theory was falsified by the Michelson-Morley experiment, but mathematicians have been classifying, tabulating, and studying knots ever since. Regarding applications, the pure mathematics of knots can find their way into cryptography, but knot theory is also intrinsically related to many aspects of the natural sciences. For example, it naturally shows up in certain spin models in statistical mechanics, when one studies thermodynamic quantities, and the magnetohydrodynamical properties of knotted magnetic fields on the surface of the sun are an important indicator of solar activity, to name a few examples. Remarkably, physical properties of knots are important in understanding the stability of macromolecular structures. This is highlighted by work of Cozzarelli and Sumners in the 1980’s, on the topology of DNA, particularly how it forms knots and supercoils. Their interdisciplinary research helped explain how enzymes untangle and manage DNA topology, crucial for replication and transcription, laying the foundation for using mathematical models to predict and manipulate DNA behavior, with broad implications in drug development and synthetic biology. Serendipitously, this work was carried out during the same decade as Richard Feynman, David Deutsch, and Yuri Manin formed the first ideas for a quantum computer.
Most importantly for our context, knot theory has fundamental connections to quantum computation, originally outlined by Witten’s work in topological quantum field theory, concerning spacetimes without any notion of distance but only shape. In fact, this connection formed the very motivation for attempting to build topological quantum computers, where anyons – exotic quasiparticles that live in two-dimensional materials – are braided to perform quantum gates. The relation between knot theory and quantum physics is the most beautiful and bizarre facts you have never heard of.
The fundamental problem in knot theory is distinguishing knots, or more generally, links. To this end, mathematicians have defined link invariants, which serve as ‘fingerprints’ of a link. As there are many equivalent representations of the same link, an invariant, by definition, is the same for all of them. If the invariant is different for two links then they are not equivalent. The specific invariant our team focused on is the Jones polynomial.

They all have the same Jones polynomial, as it is an invariant.

The mind-blowing fact here is that any quantum computation corresponds to evaluating the Jones polynomial of some link, as shown by the works of Freedman, Larsen, Kitaev, Wang, Shor, Arad, and Aharonov. It reveals that this abstract mathematical problem is truly quantum native. In particular, the problem our team tackled was estimating the value of the Jones polynomial at the 5th root of unity. This is a well-studied case due to its relation to the infamous Fibonacci anyons, whose braiding is capable of universal quantum computation.
Building and improving on the work of Shor, Aharonov, Landau, Jones, and Kauffman, our team developed an efficient quantum algorithm that works end-to end. That is, given a link, it outputs a highly optimized quantum circuit that is readily executable on our processors and estimates the desired quantity. Furthermore, our team designed problem-tailored error detection and error mitigation strategies to achieve a higher accuracy.
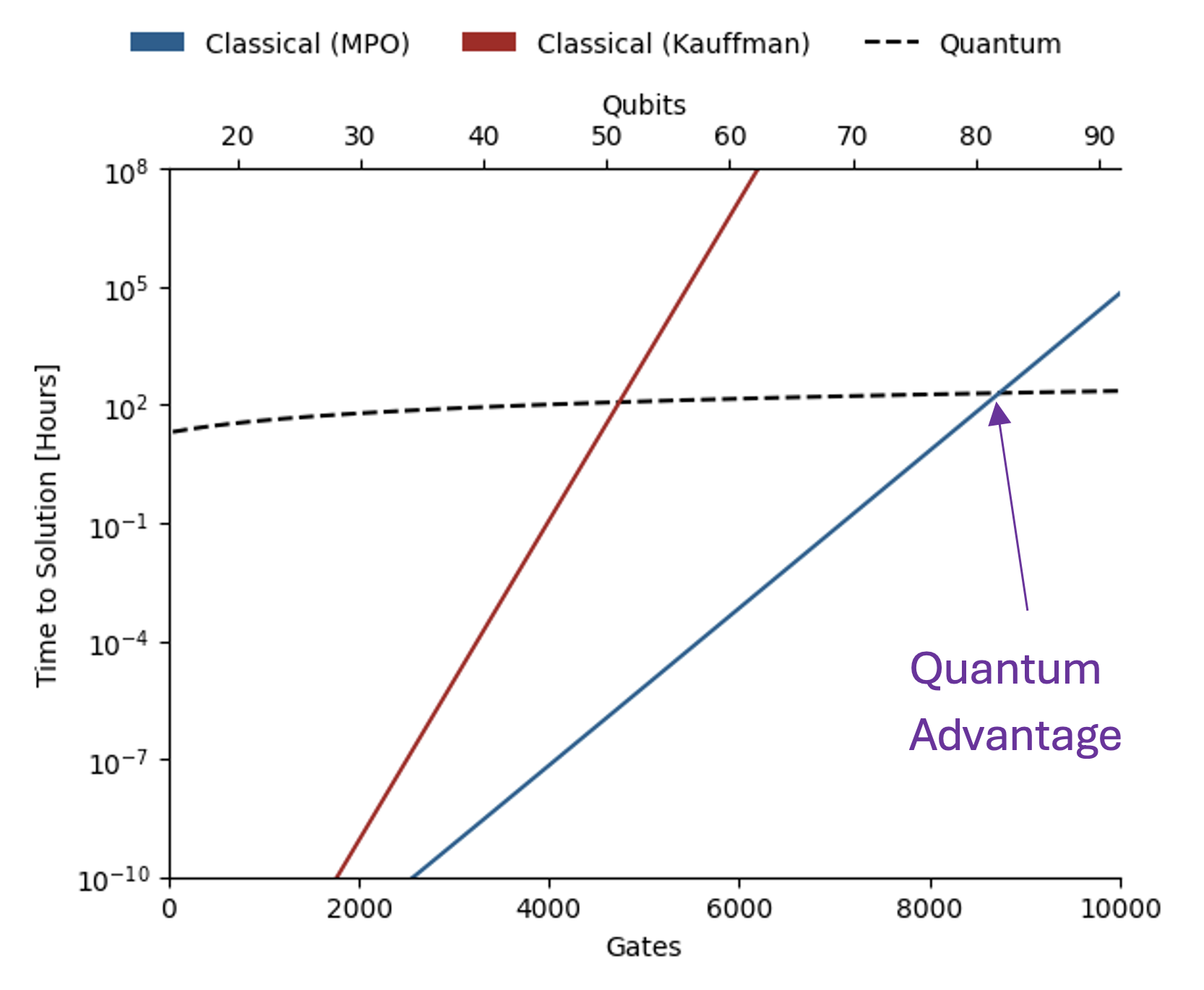
In addition to providing a full pipeline for solving this problem, a major aspect of this work was to use the fact that the Jones polynomial is an invariant to introduce a benchmark for noisy quantum computers. Most importantly, this benchmark is efficiently verifiable, a rare property since for most applications, exponentially costly classical computations are necessary for verification. Given a link whose Jones polynomial is known, the benchmark constructs a large set of topologically equivalent links of varying sizes. In turn, these result in a set of circuits of varying numbers of qubits and gates, all of which should return the same answer. Thus, one can characterize the effect of noise present in a given quantum computer by quantifying the deviation of its output from the known result.
The benchmark introduced in this work allows one to identify the link sizes for which there is exponential quantum advantage in terms of time to solution against the state-of-the-art classical methods. These resource estimates indicate our next processor, Helios, with 96 qubits and at least 99.95% two-qubit gate-fidelity, is extremely close to meeting these requirements. Furthermore, Quantinuum’s hardware roadmap includes even more powerful machines that will come online by the end of the decade. Notably, an advantage in energy consumption emerges for even smaller link sizes. Meanwhile, our teams aim to continue reducing errors through improvements in both hardware and software, thereby moving deeper into quantum advantage territory.
The importance of this work, indeed the uniqueness of this work in the quantum computing sector, is its practical end-to-end approach. The advantage-hunting strategies introduced are transferable to other “quantum-easy classically-hard” problems. Our team’s efforts motivate shifting the focus toward specific problem instances rather than broad problem classes, promoting an engineering-oriented approach to identifying quantum advantage. This involves first carefully considering how quantum advantage should be defined and quantified, thereby setting a high standard for quantum advantage in scientific and mathematical domains. And thus, making sure we instill confidence in our customers and partners.
Edited
About Quantinuum
Quantinuum, the world’s largest integrated quantum company, pioneers powerful quantum computers and advanced software solutions. Quantinuum’s technology drives breakthroughs in materials discovery, cybersecurity, and next-gen quantum AI. With over 500 employees, including 370+ scientists and engineers, Quantinuum leads the quantum computing revolution across continents.
Last year, we joined forces with RIKEN, Japan's largest comprehensive research institution, to install our hardware at RIKEN’s campus in Wako, Saitama. This deployment is part of RIKEN’s project to build a quantum-HPC hybrid platform consisting of high-performance computing systems, such as the supercomputer Fugaku and Quantinuum Systems.
Today, a paper published in Physical Review Research marks the first of many breakthroughs coming from this international supercomputing partnership. The team from RIKEN and Quantinuum joined up with researchers from Keio University to show that quantum information can be delocalized (scrambled) using a quantum circuit modeled after periodically driven systems.
"Scrambling" of quantum information happens in many quantum systems, from those found in complex materials to black holes. Understanding information scrambling will help researchers better understand things like thermalization and chaos, both of which have wide reaching implications.
To visualize scrambling, imagine a set of particles (say bits in a memory), where one particle holds specific information that you want to know. As time marches on, the quantum information will spread out across the other bits, making it harder and harder to recover the original information from local (few-bit) measurements.
While many classical techniques exist for studying complex scrambling dynamics, quantum computing has been known as a promising tool for these types of studies, due to its inherently quantum nature and ease with implementing quantum elements like entanglement. The joint team proved that to be true with their latest result, which shows that not only can scrambling states be generated on a quantum computer, but that they behave as expected and are ripe for further study.
Thanks to this new understanding, we now know that the preparation, verification, and application of a scrambling state, a key quantum information state, can be consistently realized using currently available quantum computers. Read the paper here, and read more about our partnership with RIKEN here.
In our increasingly connected, data-driven world, cybersecurity threats are more frequent and sophisticated than ever. To safeguard modern life, government and business leaders are turning to quantum randomness.
What is quantum randomness, and why should you care?
The term to know: quantum random number generators (QRNGs).
QRNGs exploit quantum mechanics to generate truly random numbers, providing the highest level of cryptographic security. This supports, among many things:
- Protection of personal data
- Secure financial transactions
- Safeguarding of sensitive communications
- Prevention of unauthorized access to medical records
Quantum technologies, including QRNGs, could protect up to $1 trillion in digital assets annually, according to a recent report by the World Economic Forum and Accenture.
Which industries will see the most value from quantum randomness?
The World Economic Forum report identifies five industry groups where QRNGs offer high business value and clear commercialization potential within the next few years. Those include:
- Financial services
- Information and communication technology
- Chemicals and advanced materials
- Energy and utilities
- Pharmaceuticals and healthcare
In line with these trends, recent research by The Quantum Insider projects the quantum security market will grow from approximately $0.7 billion today to $10 billion by 2030.
When will quantum randomness reach commercialization?
Quantum randomness is already being deployed commercially:
- Early adopters use our Quantum Origin in data centers and smart devices.
- Amid rising cybersecurity threats, demand is growing in regulated industries and critical infrastructure.
Recognizing the value of QRNGs, the financial services sector is accelerating its path to commercialization.
- Last year, HSBC conducted a pilot combining Quantum Origin and post-quantum cryptography to future-proof gold tokens against “store now, decrypt-later” (SNDL) threats.
- And, just last week, JPMorganChase made headlines by using our quantum computer for the first successful demonstration of certified randomness.
On the basis of the latter achievement, we aim to broaden our cybersecurity portfolio with the addition of a certified randomness product in 2025.
How is quantum randomness being regulated?
The National Institute of Standards and Technology (NIST) defines the cryptographic regulations used in the U.S. and other countries.
- NIST’s SP 800-90B framework assesses the quality of random number generators.
- The framework is part of the FIPS 140 standard, which governs cryptographic systems operations.
- Organizations must comply with FIPS 140 for their cryptographic products to be used in regulated environments.
This week, we announced Quantum Origin received NIST SP 800-90B Entropy Source validation, marking the first software QRNG approved for use in regulated industries.
What does NIST validation mean for our customers?
This means Quantum Origin is now available for high-security cryptographic systems and integrates seamlessly with NIST-approved solutions without requiring recertification.
- Unlike hardware QRNGs, Quantum Origin requires no network connectivity, making it ideal for air-gapped systems.
- For federal agencies, it complements our "U.S. Made" designation, easing deployment in critical infrastructure.
- It adds further value for customers building hardware security modules, firewalls, PKIs, and IoT devices.
The NIST validation, combined with our peer-reviewed papers, further establishes Quantum Origin as the leading QRNG on the market.
--
It is paramount for governments, commercial enterprises, and critical infrastructure to stay ahead of evolving cybersecurity threats to maintain societal and economic security.
Quantinuum delivers the highest quality quantum randomness, enabling our customers to confront the most advanced cybersecurity challenges present today.
The most common question in the public discourse around quantum computers has been, “When will they be useful?” We have an answer.
Very recently in Nature we announced a successful demonstration of a quantum computer generating certifiable randomness, a critical underpinning of our modern digital infrastructure. We explained how we will be taking a product to market this year, based on that advance – one that could only be achieved because we have the world’s most powerful quantum computer.
Today, we have made another huge leap in a different domain, providing fresh evidence that our quantum computers are the best in the world. In this case, we have shown that our quantum computers can be a useful tool for advancing scientific discovery.
Understanding magnetism
Our latest paper shows how our quantum computer rivals the best classical approaches in expanding our understanding of magnetism. This provides an entry point that could lead directly to innovations in fields from biochemistry, to defense, to new materials. These are tangible and meaningful advances that will deliver real world impact.
To achieve this, we partnered with researchers from Caltech, Fermioniq, EPFL, and the Technical University of Munich. The team used Quantinuum’s System Model H2 to simulate quantum magnetism at a scale and level of accuracy that pushes the boundaries of what we know to be possible.
As the authors of the paper state:
“We believe the quantum data provided by System Model H2 should be regarded as complementary to classical numerical methods, and is arguably the most convincing standard to which they should be compared.”
Our computer simulated the quantum Ising model, a model for quantum magnetism that describes a set of magnets (physicists call them ‘spins’) on a lattice that can point up or down, and prefer to point the same way as their neighbors. The model is inherently “quantum” because the spins can move between up and down configurations by a process known as “quantum tunneling”.
Gaining material insights
Researchers have struggled to simulate the dynamics of the Ising model at larger scales due to the enormous computational cost of doing so. Nobel laureate physicist Richard Feynman, who is widely considered to be the progenitor of quantum computing, once said, “it is impossible to represent the results of quantum mechanics with a classical universal device.” When attempting to simulate quantum systems at comparable scales on classical computers, the computational demands can quickly become overwhelming. It is the inherent ‘quantumness’ of these problems that makes them so hard classically, and conversely, so well-suited for quantum computing.
These inherently quantum problems also lie at the heart of many complex and useful material properties. The quantum Ising model is an entry point to confront some of the deepest mysteries in the study of interacting quantum magnets. While rooted in fundamental physics, its relevance extends to wide-ranging commercial and defense applications, including medical test equipment, quantum sensors, and the study of exotic states of matter like superconductivity.
Instead of tailored demonstrations that claim ‘quantum advantage’ in contrived scenarios, our breakthroughs announced this week prove that we can tackle complex, meaningful scientific questions difficult for classical methods to address. In the work described in this paper, we have proved that quantum computing could be the gold standard for materials simulations. These developments are critical steps toward realizing the potential of quantum computers.
With only 56 qubits in our commercially available System Model H2, the most powerful quantum system in the world today, we are already testing the limits of classical methods, and in some cases, exceeding them. Later this year, we will introduce our massively more powerful 96-qubit Helios system - breaching the boundaries of what until recently was deemed possible.